Last modified on May 9th, 2025 at 10:41 am
We’re used to thinking of distance as looking out horizontally towards the horizon. That applies to many infrared imaging scenarios, but not all.
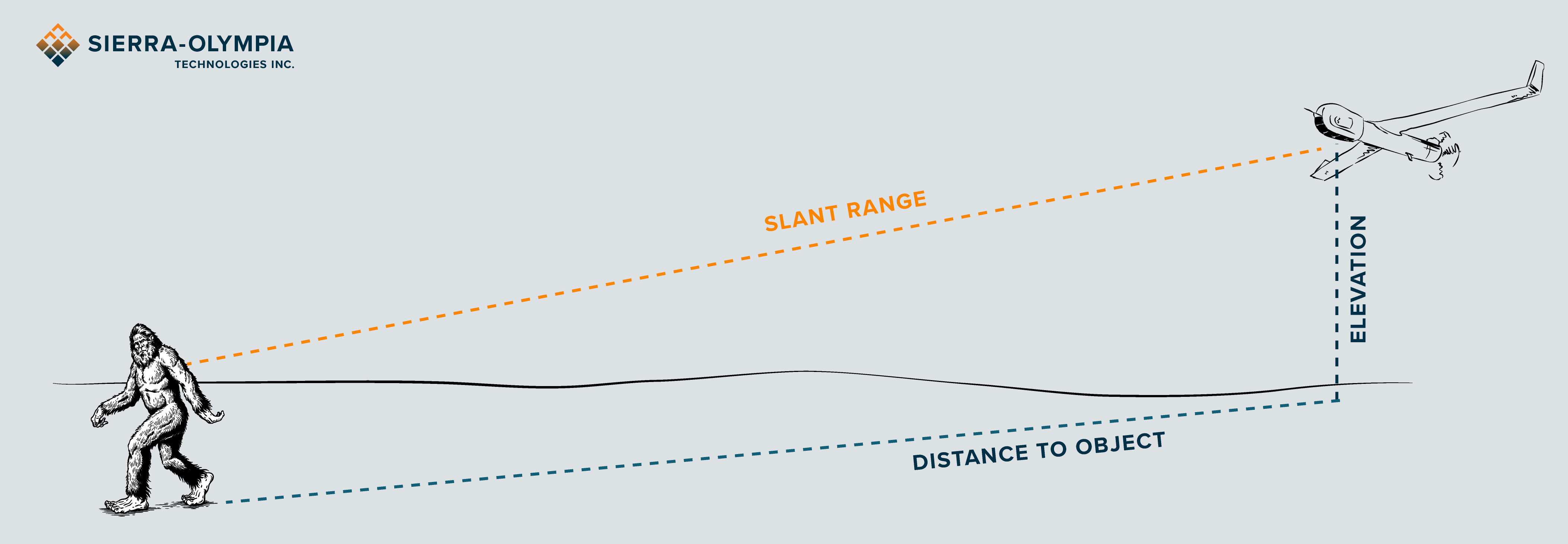
Today, we’re going to be talking about something called slant range. Slant range is the distance from a camera to an object being imaged. It takes into account the geometry of the camera and object being imaged at different altitudes. One example is where we might have a camera on an airborne platform looking at an object on the ground.
Why is distance important in infrared imaging?
When we design an infrared imaging system we think about the field of view (FOV) of the camera. The distance to the object tells us how much of the field of view we’re going to be able to see at any distance. Another factor related to that is called instantaneous field of view (iFOV). That’s the field of view of a single pixel, which tells us how many pixels we will get on a certain object at that distance. That tells us how well we’ll be able to resolve that object at that distance. For more information on iFOV, read our previous Ask an Expert on FOV and iFOV.

A real world scenario
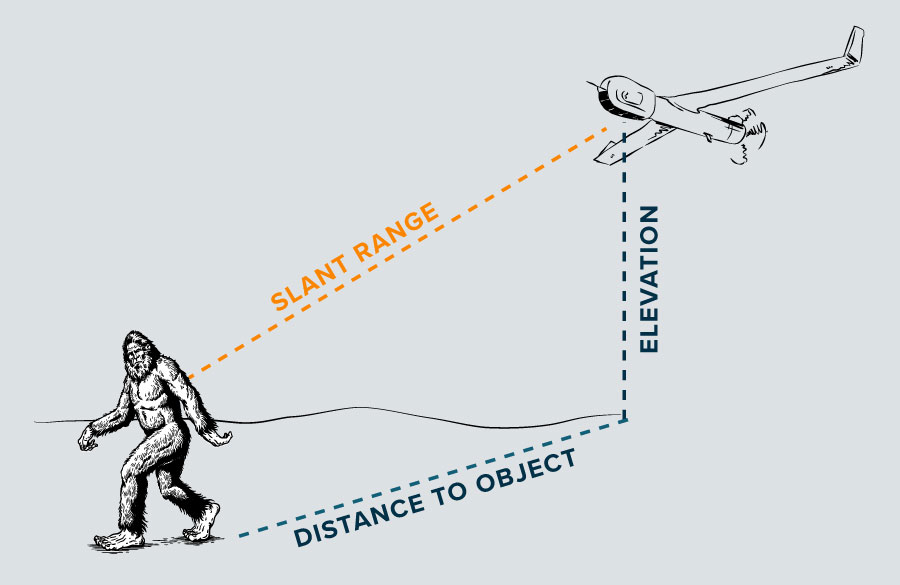
Let’s look at the slant range, the field of view, and the instantaneous field of view or the IFOV. In Figure A we’ve got an drone that’s looking over an exaggerated Sasquatch. The drone’s elevation is one leg of a vertical right triangle. The horizontal distance that was mentioned at the beginning (distance to object) is the other leg of that right triangle. Using basic geometry the Pythagorean theorem tells us what the slant range is going to be in this case.
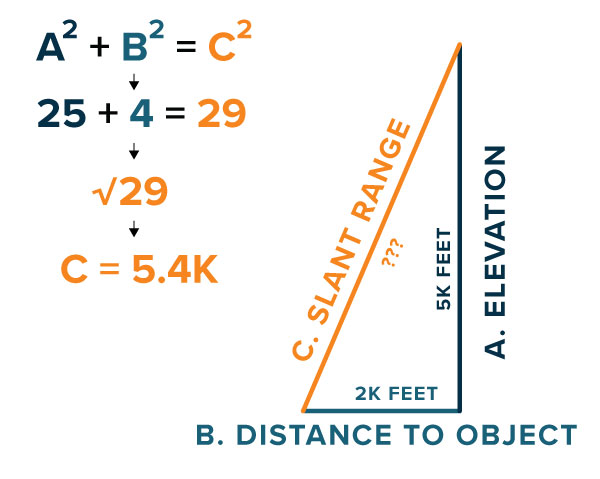
Let’s add some numbers to this scenario. We’ll estimate that this aircraft is flying at about 5000 feet. Simplify it by calling it 5K, and that the object is about a horizontal distance of 2K feet away. Now we have a right triangle as shown in Figure B. Going back to our Pythagorean theorem and our geometry, A squared plus B squared and we’ll find the slant range, which equals C squared. 5 squared is 25. 2 squared is 4. Add those together and we get 29. Then take the square root of 29 which is 5.4 when rounded to the nearest 10th. We’re working in thousands of feet so that tells us that our slant range here is about 5,400 feet. That’s the slant range from our imager to the object.
Slant Range Can Change
You’ll notice in this example, the altitude and the slant range are very close to each other. That’s because in this example, this aircraft is currently looking at a very high, very steep downward angle. At those very steep angles, the slant range is going to be dominated by the altitude. In the Figure A example our imager would be on a gimbal. So as the gimbal moves its imager up to a more shallow imaging angle, the slant range will become more dominated by the horizontal distance. The vertical distance still factors in, but at a shallower imaging angle, the horizontal distance becomes much more of a factor in that calculation.
In summary, slant range is just the distance from the imager to the object, but it takes into account the geometry of the imager being at an altitude instead of just looking horizontally across the ground. Thank you for reading this Ask an Expert.